Stereometry

In this activity, we explore another method in 3d reconstruction, called stereometry. In this method, we try to reconstruct a 3d object using 2 images of it taken by the same camera at the same distance but with a different x position (assuming x is the parallel axis between the camera and the object). Using the same reference points (which I indicated by drawing dots on the graphing paper) from the 2 images, we can compute the z-axis or depth information.
The object I used was a graphing paper shaped like a box. The difference between the x axis position is 29mm.

Since the focal length is automatically computed by the camera I used, I did not use the RQ factorization. The x values for the reference on both images and the calculated z values are tabulated below.

x1	x2	z
128.519	47.0919	−13.814
114.150	75.8309	−29.354
132.625	72.4096	−18.680
147.678	92.2532	−20.294
141.52	76.5152	−17.304
169.575	118.255	−21.918
168.206	105.254	−17.868
166.153	95.6745	−15.960
203.104	149.047	−20.808
203.788	145.626	−19.339
218.157	153.152	−17.304
220.210	153.152	−16.774
253.055	191.471	−18.265
253.055	203.104	−22.518
266.056	214.052	−21.629
271.530	214.736	−19.805
287.268	220.210	−16.774
282.478	233.895	−23.153
316.691	262.634	−20.808
312.586	264.003	−23.153
350.904	292.058	−19.114
360.484	296.163	−17.488
383.749	322.849	−18.470
363.221	311.901	−21.918

Using linear interpolation, to fill in the gaps between reference points, and the cshep function(cubic scattered interpolation), I tried a 3d reconstruction of the object.

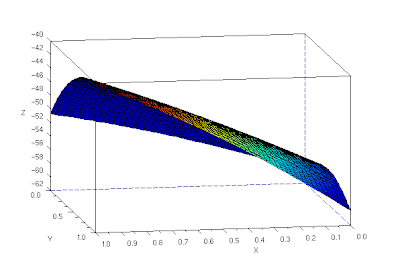The 3d reconstruction is not that good (3d reconstructed image shown is not in the same angle as the original images). The corner is curved and the fold is not straight.
//Scilab code
b = 28.34;
f = 39.69;
d1 = fscanfMat("coords-image1.txt");
d2 = fscanfMat("coords-image2.txt");
x1 = d1(1, :);
x2 = d2(1, :);
y = d2(2, :);
z = b*f./((x2 - x1) + 0.00001);
x = x1;
np = 50;
xp = linspace(0,1,np); yp = xp;
[XP, YP] = ndgrid(xp,yp);
xyz = [x' y' z'];
XP = XP*40;
YP = YP*40;
ZP1 = eval_cshep2d(XP, YP, cshep2d(xyz));
xset("colormap", jetcolormap(64))
xbasc()
plot3d1(xp, yp, ZP1, flag=[2 2 4])
//code end

I give myself a grade of 7 since the blog was very late. :(
Thanks to Benj Palmares for the tip on using cshep instead of spline2d.